Analytical Solution to Global Dynamic Balance Control of the Acrobot

Abstract

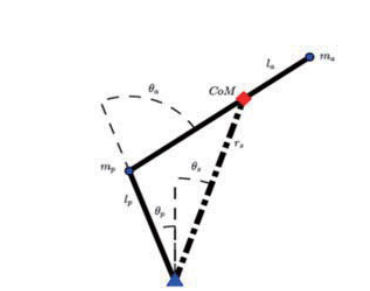
To provide a high level dynamic stability objective for humanoid robots that takes into consideration forces due to joint coupling, we derive an analytical solution to the dynamic balance control of the Acrobot, a fixed-base underactuated inverted double pendulum. We will show that the proof for stability involves an analogy to the dynamic stabilization of a rigid pendulum through vertical vibrations of its base, thus providing physical and mathematical insights into controls and dynamic stability of underactuated, articulated systems like the humanoid robot.